Tree data structure: Binary Search Tree
Tree data structures are non-linear data structures, and they allow us to implement algorithms much faster than when using linear data structures.
Tree
A tree is a data structure that consists of nodes connected by edges.
Binary tree
A Binary tree can have two children: a left node and a right node. Every Node contains two elements: a key used to identify the data stored by the Node and a value that is the data contained in the Node. The following figure shows the binary tree terminology.
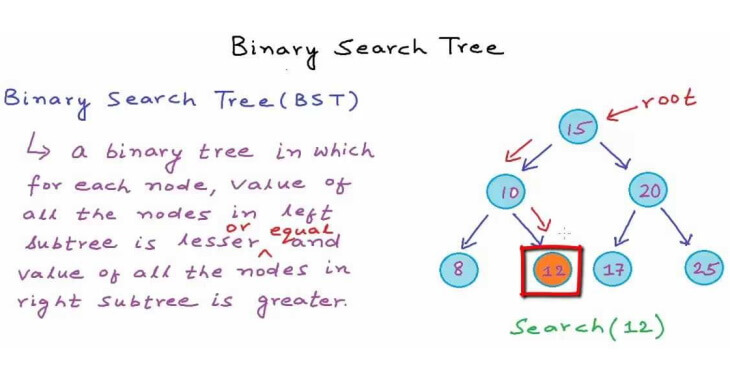
Binary search tree
The most common type of Binary tree is the Binary search tree, which has two main characteristics:
- The value of the left Node must be lesser than the value of its parent.
- The value of the right Node must be greater than or equal to the value of its parent.
Moreover, you can search in a tree data structure quickly, as you can with an ordered array, and you can also insert and delete items quickly, as you can with a linked list.
It takes a maximum of log2(N) attempts to find a value. As the collection of nodes gets large, the binary search tree becomes faster over a linear search which takes up to (N) comparisons.
Tree data structure: Use Case:
The Global Trade Item Number (GTIN) can be used by a company to uniquely identify all of its trade items.
The GTIN can be used to identify types of products that are produced by different manufacturers.
A Webshop wants to retrieve information about GTINs efficiently by using a binary search algorithm.
Solution:
We create a Product Class which will be the data contained in a Node.
1
2
3
4
5
6
7
8
9
public class Product {
Integer productId;
String name;
Double price;
String manufacturerName;
.
//code omitted for brevity
}
We create a NodeP Class to store a list of Products. Moreover, this Class allows us to have two NodeP attributes to hold the left and right nodes.
1
2
3
4
5
6
7
8
9
10
11
12
public class NodeP {
private String gtin;
private List<Product> data;
private NodeP left;
private NodeP right;
public NodeP(String gtin, List<Product> data) {
this.gtin = gtin;
this.data = data;
}
}
We create a new abstract data type called TreeP to define the behavior of our Binary Search Tree, which includes a NodeP root variable for the first element to be inserted.
We need to implement an insert method, where every time a new GTIN is inserted, it compares the current GTIN versus the new GTIN. We store the new GTIN on the left or the right Node, depending on the result. In this way, the insert method maintains an ordered binary search tree.
A Test case to verify our assumptions:
1
2
3
4
5
@Test
public void when_rootNull_inserNode() {
tree.insert("04007801321224", new ArrayList<>(Arrays.asList(product1)));
assertTrue(tree.getRoot() != null);
}
And here the implementation for the insert method:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
public class TreeP {
private NodeP root;
public void insert(String gtin, List<Product> data) {
NodeP newNode = new NodeP(gtin, data);
if (root == null)
root = newNode;
else {
NodeP current = root;
NodeP parent;
while (true) {
parent = current;
if (gtin.compareTo(current.getGtin()) < 0) {
current = current.getLeft();
if (current == null) {
parent.setLeft(newNode);
return;
}
} else if (gtin.compareTo(current.getGtin()) > 0) {
current = current.getRight();
if (current == null) {
parent.setRight(newNode);
return;
}
} else
current.setData(data);
return; //already exists
}
}
return;
}
}
Create a Test case for a find method:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
@Test
public void test_findNode() {
tree.insert("04000345706564",
new ArrayList<>(Arrays.asList(product1)));
tree.insert("07611400983416",
new ArrayList<>(Arrays.asList(product2)));
tree.insert("07611400989104",
new ArrayList<>(Arrays.asList(product3, product4)));
tree.insert("07611400989111",
new ArrayList<>(Arrays.asList(product5)));
tree.insert("07611400990292",
new ArrayList<>(Arrays.asList(product6, product7, product8)));
assertEquals(null, tree.find("07611400983324"));
tree.insert("07611400983324",
new ArrayList<>(Arrays.asList(product9)));
assertTrue(tree.find("07611400983324") != null);
assertEquals("07611400983324",
tree.find("07611400983324").getGtin());
}
And here is the implementation that shows a find method (the gtin parameter is our key), which iterates through all nodes until a GTIN is found. This algorithm reduces the search space to N/2 because the binary search tree is always ordered.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public NodeP find(String gtin) {
NodeP current = root;
if (current == null)
return null;
while (!current.getGtin().equals(gtin)) {
if (gtin.compareTo(current.getGtin()) < 0) {
current = current.getLeft();
} else {
current = current.getRight();
}
if (current == null) //not found in children
return null;
}
return current;
}
This Binary Search Tree works well when the data is inserted in random order. Therefore, when the values to be inserted are already ordered, a binary tree becomes unbalanced. With an unbalanced tree, we can not find data quickly.
One approach to solving unbalanced trees is the red-black tree technique, which is a binary search tree with some special features.
Assuming that we already have a balanced tree, the following algorithm shows us how fast in terms of comparisons could be a binary search tree which depends on a number N of elements. For instance, in 1 billion products, to find a product by GTIN, the algorithm needs only 30 comparisons. See Big O Notation.
1
2
3
4
5
6
7
@Test
public void whenNelements_return_NroComparisons(){
assertTrue(treePerformance.comparisons(15) <= 4);
assertTrue(treePerformance.comparisons(31) <= 5);
assertTrue(treePerformance.comparisons(1000) <=10);
assertTrue(treePerformance.comparisons(1000000000) <=30);
}
And here is our implementation.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public class TreePerformance {
public static int comparisons(int N) {
int acumElements = 0;
int comparisons = 0;
for (int level = 0; level <= N / 2; level++) {
int power = (int) Math.pow(2, level);
acumElements += power;
if (acumElements >= N) {
comparisons = ++level;
break;
}
}
System.out.println("comparisons -> " + comparisons);
return comparisons;
}
}
Understanding the inner workings of common data structures and algorithms is a must for Java developers. Learn more

