Big O Notation and Analysis of Algorithms - coding interview

Big O Notation is a mathematical notation that helps us analyze how complex an algorithm is in terms of time and space. When we build an application for one user or millions of users, it matters.
We implement different algorithms to solve one problem and measure how efficient is one respect to the other ones.
Algorithm analysis is an essential part of computational complexity theory, which aims to quantify the resources required to solve computational problems.
The first study about Analysis of Algorithms was published by Knuth in 1968. The Art of Computer Programming.
Asymptotic Notation is used to describe the running time of an algorithm. There are three different notations: Big Omega, Big Theta, and Big O Notation.
Time complexity analysis and space complexity analysis
Time complexity analysis is related to how many steps takes an algorithm.
Space complexity analysis is related to how efficient an algorithm is using the memory and disk.
Both terms depend on the input size, the number of items in the input. Both terms depend on the input size and the number of items in the input. Moreover, we can analyze the complexity based on three cases or asymptotic notations.:
-
Best case or Big Omega Ω(n): Usually the algorithm executes in one step independently of the input size.
-
Average case or Big Theta Θ(n): If the the input size is ramdom
-
Worst-case analysis or Big O Notation O(n): Gives us an upper bound on the runtime for any input. It gives us a kind of guarantee that the algorithm will never take any longer with a new input size.
Order of growth
The order of growth is related to how the runtime of an algorithm increases when the size of the input increases without limit and tells us how efficient the algorithm is.
In essence, Big O notation provides a worst-case scenario for an algorithm’s performance, allowing developers to compare different algorithms and choose the most efficient one for large inputs.
Big O Notation: Common order-of-growth classifications:
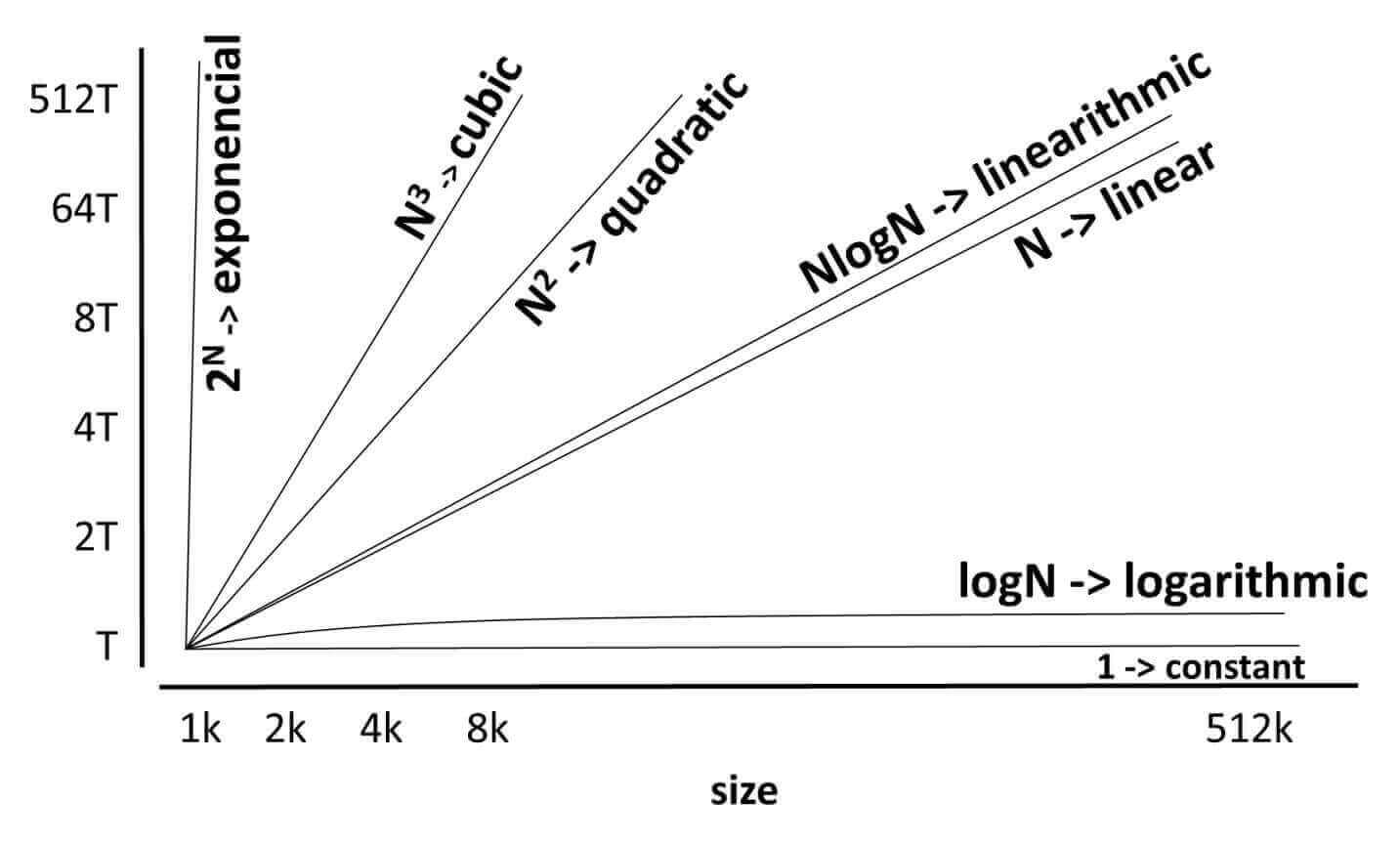
Big O Notation: examples
O(1) – Constant Time Complexity
The runtime does not change with the size of the input. It does not matter if the input contains 1000 or 1 million items, the code always executes in one step.
1
2
3
public void constant(List<string> list, String item) {
list.add(item);
}
In a best-case scenario, an add method takes O(1) time. The worst-case scenario takes O(n).
O(N) – Linear Time Complexity
An algorithm runs in O(N) time if the number of steps depends on the number of items included in the input. The runtime grows linearly with the size of the input.
Example: Iterating through an array or a list.
1
2
3
4
5
6
7
public int sum(int[] numbers) {
int sum =0;
for (int i =0; i<numbers.length; i++) {
sum+=numbers[i]; // Iterating through each element
}
return sum;
}
In this example, if numbers has n elements, the loop executes n times, so the time complexity is O(n).
The main idea in Analysis of Algorithms is always to improve the algorithm performance, by reducing the number of steps and comparisons. You can visit find the smallest number with the same number of digits, for instance. Moreover, the simpler and more intuitive an algorithm is, the more useful and efficient it will be.
O(N2) – Quadratic Time Complexity
If an algorithm includes two loops nested in its code, we could say that it’s running in quadratic time O(N2). The runtime grows quadratically with the size of the input.
Example: When a 2D matrix is initialized in a tic-tac-toe game.
1
2
3
4
5
6
7
8
9
10
private String [][] board;
public void initializeBoard(int size) {
this.board = new String[size][size];
for (int x = 0; x < size; x++) {
for (int y = 0; y < size; y++) {
board[x][y] = " ";
}
}
}
Example: Nested loops iterating over the same collection
1
2
3
4
5
6
int[] arr = {1, 2, 3, 4, 5};
for (int i = 0; i < arr.length; i++) {
for (int j = 0; j < arr.length; j++) {
System.out.println(arr[i] + " " + arr[j]); // Nested loop
}
}
Here, if arr has n elements, the outer and inner loops both run n times, resulting in n * n = n2, so the complexity is O(N2).
Pragmatic Programmer, The: Your journey to mastery, 20th Anniversary Edition https://t.co/MwIRotEMY4 via @amazon
— Moises Gamio (@MoisesGamio) November 8, 2024
O(N3) – Cubic Time Complexity
When the code includes at the most three nested loops, then the algorithm runs in Cubic time.
Example: Given N integers, how many triples sum to exactly zero?. One approach (not the best) is to use three nested loops.
1
2
3
4
5
6
7
8
9
10
11
public int countThreeSum(int[] numbers) {
int N =numbers.length;
int count =0;
for (int i = 0; i<N; i++)
for (int j = i+1; j<N; j++)
for (int k = j+1; k<N; k++)
if (numbers[i] + numbers[j] + numbers[k] == 0)
count++;
return count;
}
O(LogN) – Logarithmic Time Complexity
This kind of algorithm produces a growth curve that peaks at the beginning and slowly flattens out as the size of the input increase. The runtime grows logarithmically with the input size.
Example: Binary search on a sorted array.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int binarySearch(int[] arr, int target) {
int left = 0;
int right = arr.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (arr[mid] == target) {
return mid;
} else if (arr[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return -1; // Element not found
}
Log28 = 3
Log216 = 4
Log232 = 5
The binary search uses at most LogN key compares to search in a sorted array of size N. With 8 elements, it takes three comparisons, with 16 elements takes four comparisons, with 32 elements takes five comparisons, and so on.
In this example, with each iteration, the search space is halved. This results in a time complexity of O(LogN).
You can read more common Big O notations such as Linearithmic Time Complexity (O(n log n)), Exponential Time Complexity (O(2n)), and many more in the following link:
Summary of Big O Complexity Types:
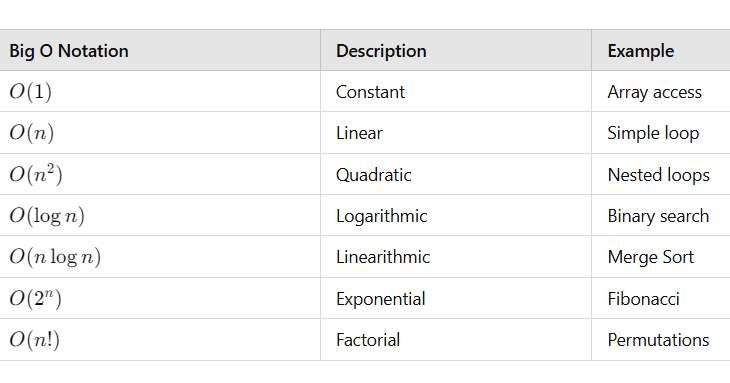
Big O notation is essential to understand the scalability and efficiency of algorithms, especially for large datasets or performance-critical applications.
The complexity of an algorithm
To find the Big O complexity of an algorithm follows the following rules:
- Ignore the lower order terms
- Drop the leading constants
Example: If the time complexity of an algorithm is 2n3 + 4n + 3. Its Big O complexity simplifies to O(n3).
How to find the time complexity of an algorithm
Given the following algorithm:
1
2
3
4
5
6
7
8
public Integer sumEvenNumbers(Integer N) {
int sum = 0;
for (int number = 1; number <= N; number++)
if ((number % 2) == 0)
sum = sum + number;
return sum;
}
First, we split the code into individual operations and then compute how many times it is being executed as is shown in the following table.
| Description | Number of executions |
|---|---|
| int sum = 0; | 1 |
| int number = 1; | 1 |
| number <= N; | N |
| number++ | N |
| if ((number % 2) == 0) | N |
| sum = sum + number; | N |
| return sum; | 1 |
Now, we need to sum up how many times each operation is executing.
Time complexity = 1 + 1 + N + N + N + N + 1 => 4N + 3
Why Big O Notation ignores constants?
Big O Notation describes how many steps are required relative to the number of data elements. And it serves as a way to classify the long-term growth rate of algorithms.
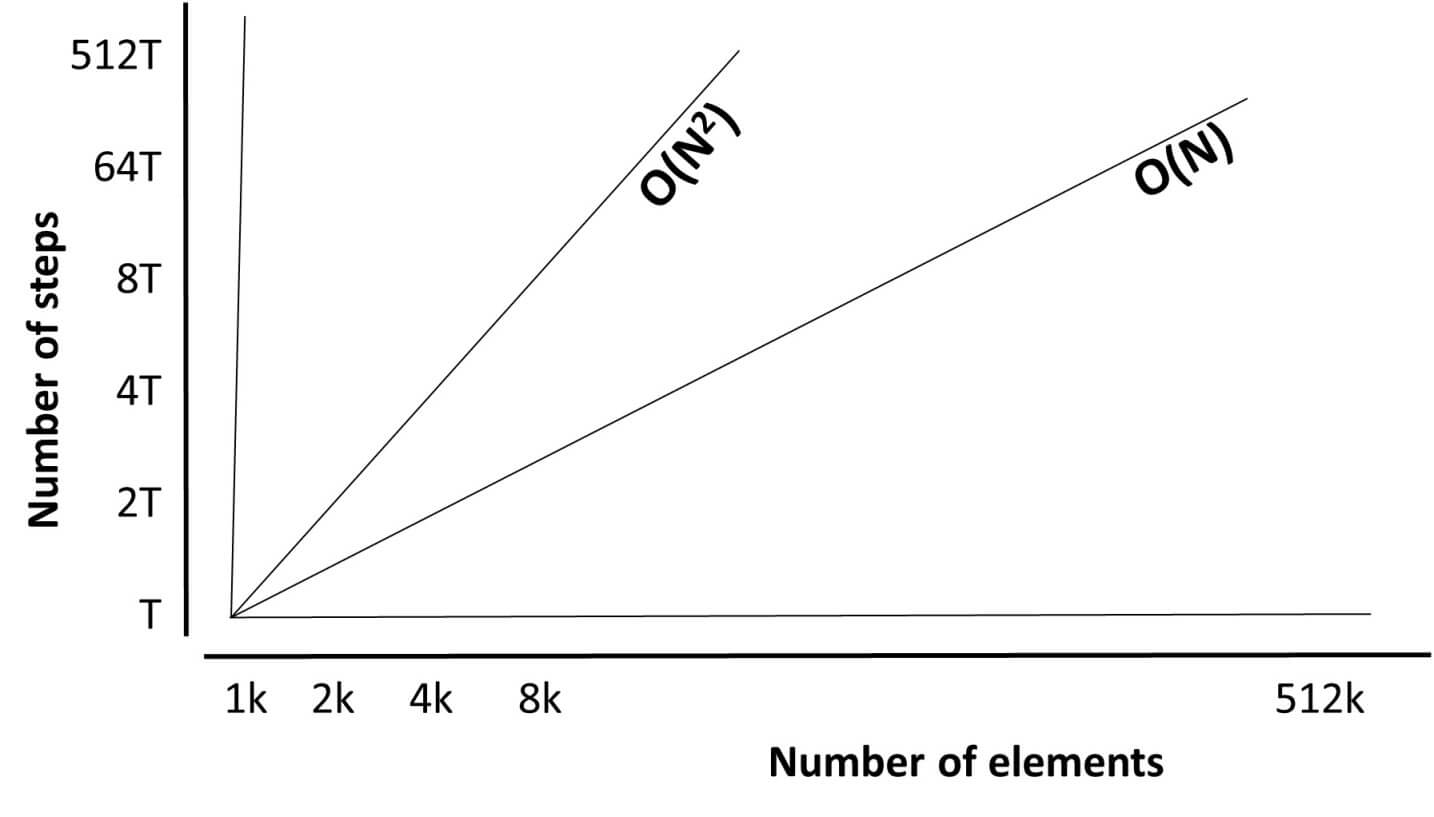
For instance, for all amounts of data, O(N) will be faster than O(N2) as shown in the following figure:
Now, if we compare O(100N) with O(N2), we can see that O(N2) is faster than O(100N) for some amounts of data as shown in the following figure:
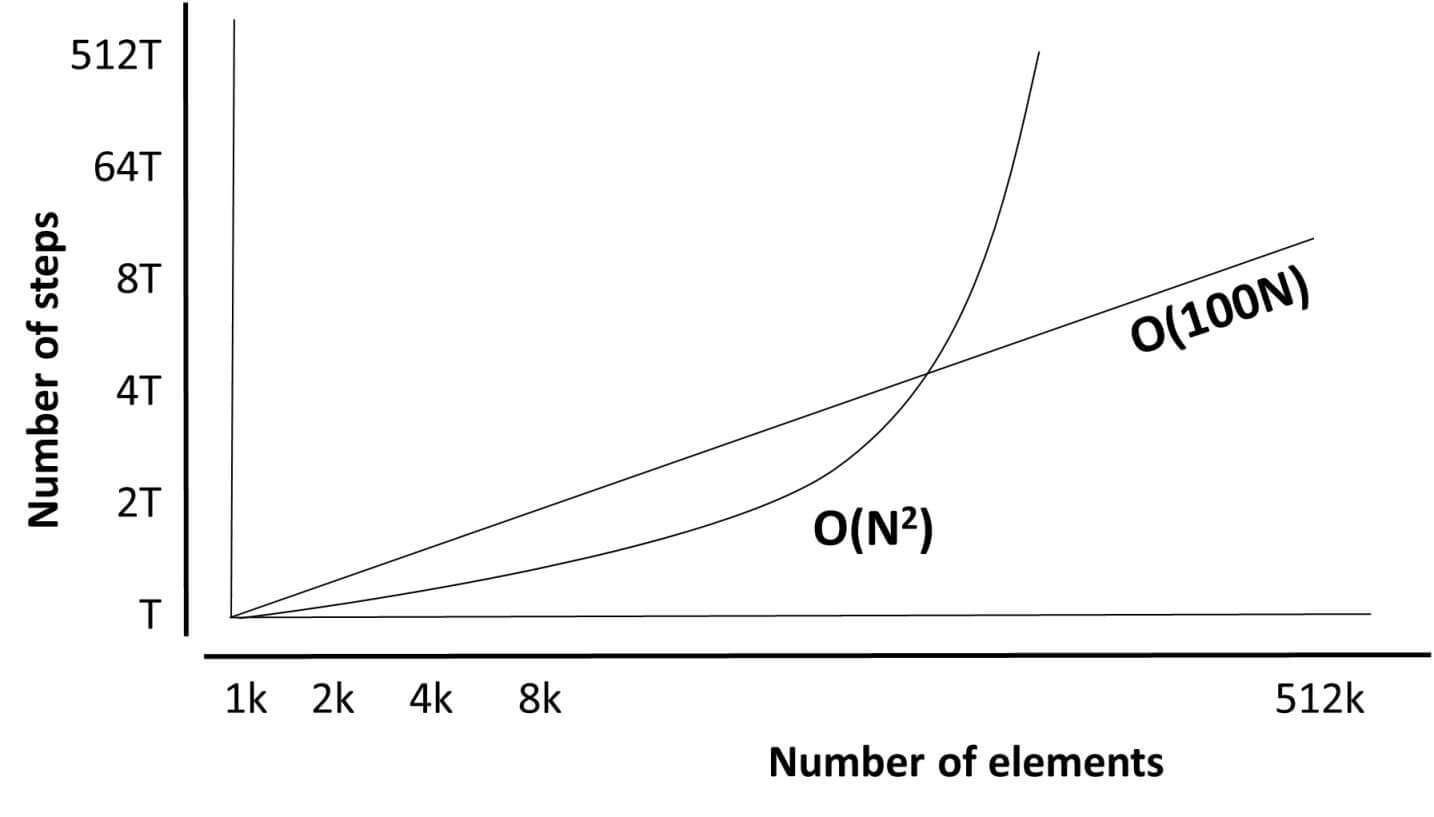
But after an intersection point, O(100N) becomes faster and remains faster (in terms of the “number of steps”) for all increasing amounts of data from that point onward. And that is the reason why Big O Notation ignores constants. Because of this, the value of 100 is irrelevant and O(100N) is written as O(N). The fewer steps, the faster the algorithm.
Introduction to Algorithms, fourth edition https://t.co/d6ThijT6Za via @amazon
— Moises Gamio (@MoisesGamio) September 25, 2024
This article was just an introduction to algorithm analysis to face an actual code interview as a software developer. They are asked to build approximated models using Big O notation in Java. The same concepts apply to Python algorithm analysis.
If you want to create a mathematical model for the execution time of a discrete operation, for example, you should take a course in discrete mathematics.
Please donate to maintain and improve this website if you find this content valuable.
Preparing to discuss algorithms analysis in your following programming interview requires practicing and studying different algorithms, and you can find it in Cracking the Coding Interview with many explanation details.


