Combinational Optimization Problem
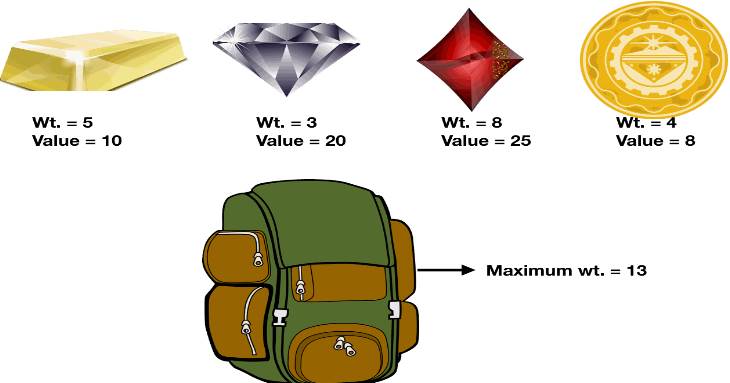
The Knapsack problem is a classic optimization problem in computer science and mathematics. It belongs to a class of problems known as combinatorial optimization problems. The basic idea of the Knapsack problem is to determine the most valuable combination of items to include in a knapsack, given their weights and values, without exceeding the capacity of the knapsack.
Greedy Algorithm
A greedy algorithm is an algorithmic paradigm that makes locally optimal choices at each stage with the hope of finding a global optimum. The idea is to make the best possible choice at each step without worrying about the future consequences. Greedy algorithms are often used for optimization problems where you need to make a series of decisions, and at each decision point, you choose the option that seems most promising at that moment.
One classic example of a greedy algorithm is the “Fractional Knapsack Problem.” In this problem, you are given a set of items, each with a weight and a value, and you want to fill a knapsack with a maximum weight capacity to maximize the total value of the items you select.
Backtracking Algorithm
Backtracking is a general algorithm for finding all (or some) solutions to computational problems, particularly constraint satisfaction problems. It incrementally builds candidates for solutions, and abandons a candidate (“backtracks”) as soon as it determines that the candidate cannot possibly be completed to a valid solution.
Backtracking is often used when a problem can be broken down into a series of smaller decisions, and it is not clear which decision is the correct one. The algorithm explores different choices one at a time, and if it determines that a particular choice cannot lead to a valid solution, it goes back (hence the term “backtracking”) to the previous decision point and explores a different choice.
Backtracking is used to explore different arrangements until a valid solution is found or all possibilities are exhausted.
Problem
Fill a basket with the most valuable goods under a given budget to optimize online purchases.
Imagine that we have a budget of 4 US$ and we want to buy the most valuable snacks from the following table:
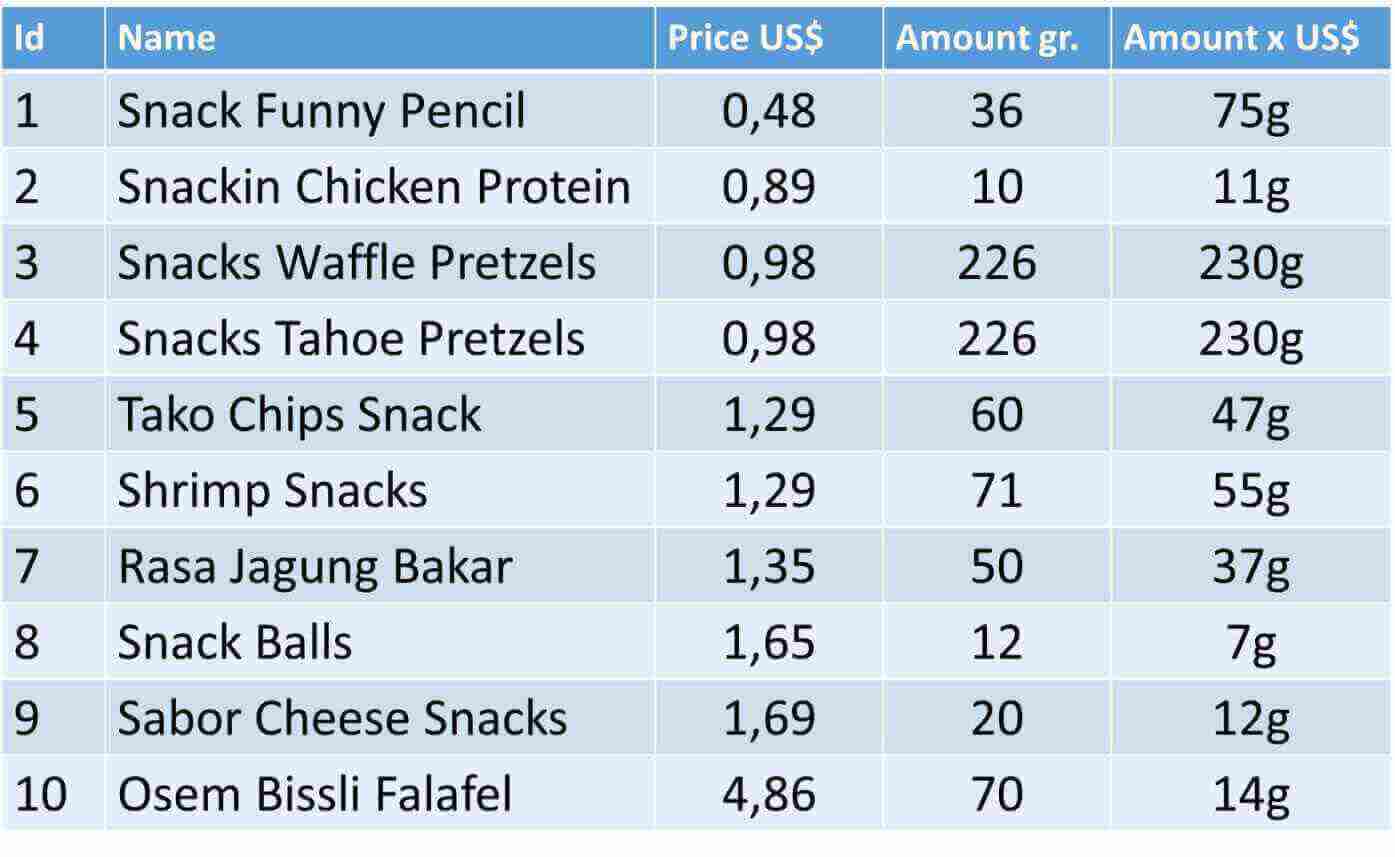
But who decides if a product is more valuable than another one? Well, this depends on every business. It could be an estimation based on quantitative or qualitative analysis. For instance, for our solution, we choose a quantitative approach based on which product gives us more grams per every dollar invested.
Optimize a basket in online purchases: Solution
To implement our algorithm to optimize a basket in online purchases, we use the Red-Green Refactor technique, which is the basis of test-drive-development (TDD). Firstly, in every assumption, we will write a test and see if it fails. Secondly, we write the code that implements only that test and sees if it succeed, then we can refactor the code to make it better. Finally, we continue with another assumption and repeat the previous steps until the algorithm is successfully implemented for all tests.
To generalize the concept of “the most valuable product” we assign a value to every product. Our algorithm receives two parameters: a 2-D array which includes [product-id][price][value] and the budget.
Assumption #1 – Given an array of products ordered by value, return the most valuable products
We start defining a java test creating a new BasketOptimized class. For naming variables, you can read clean code.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
public class BasketOptimizedTest {
BasketOptimized basketOptimized;
@Before
public void setup() {
basketOptimized = new BasketOptimized();
}
@Test
public void productsOrderedByValue () {
double[][] myProducts = new double[][] {
{1, 0.98, 230},
{2, 0.98, 230},
{3, 0.48, 75},
{4, 1.29, 55},
{5, 1.29, 47},
{6, 4.86, 14},
{7, 1.69, 12},
};
double[][] mostValueableProducts =
basketOptimized.fill(myProducts, 4);
assertEquals(590d,
Arrays.stream(mostValueableProducts).
mapToDouble(arr -> arr[2]).sum(),0);
}
}
The first time, it should fail because the fill method doesn’t exist. Then we need to create an easy implementation to pass the test: the sum of the values must be equal to 590 because this represents all selected products which its prices sum less or equal than 4.
Now, we proceed to implement the fill method.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public class BasketOptimized {
public double[][] fill(double[][] myProducts, double budget) {
int len = myProducts.length;
double[][] mostValueableProducts = new double[len][3];
double sum = 0;
for (int idx=0; idx < len; idx++) {
sum = sum + myProducts[idx][1]; //price
if (sum <= budget) {
mostValueableProducts[idx][0] =
myProducts[idx][0]; //id
mostValueableProducts[idx][1] =
myProducts[idx][1]; //price
mostValueableProducts[idx][2] =
myProducts[idx][2]; //value
}
}
return mostValueableProducts;
}
}
Assumption #2 – Given an array of products not ordered by value, return the most valuable products
In this case we pass a not ordered array, so we can see that our new test will fail.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
@Test
public void productsNotOrderedByValue () {
double[][] myProducts = new double[][]{
{1, 0.98, 230},
{2, 1.29, 47},
{3, 1.69, 12},
{4, 1.29, 55},
{5, 0.98, 230},
{6, 4.86, 14},
{7, 0.48, 75}
};
double[][] mostValueableProducts
= basketOptimized.fill(myProducts, 4);
assertEquals(590d, Arrays.stream(mostValueableProducts)
.mapToDouble(arr -> arr[2]).sum(), 0);
}
Any software design is generally a matter of opinion. There is no definitive Guide. – codersite.dev
We realize that we need to order the array by value because we want the most valuable products, so its time to refactor our algorithm. What we need to do is to sort our input array.
1
2
3
4
5
6
public double[][] fill(double[][] myProducts, double budget) {
Arrays.sort(myProducts, Collections.reverseOrder(
Comparator.comparingDouble(a -> a[2])));
int len = myProducts.length;
double[][] mostValueableProducts = new double[len][3];
Then we can see our two test cases were successful.
Calculate combinations
Assumption #3 – Given an array of products, we need to obtain the most valuable products from all possible combinations of the products
Imagine the following scenario:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
double[][] myProducts = new double[][] {
{1, 0.98, 230},
{2, 0.51, 30},
{3, 0.49, 28},
{4, 1.29, 55},
{5, 0.98, 230},
{6, 4.86, 14},
{7, 0.48, 75},
};
double[][] mostValueableProducts = basketOptimized
.fill(myProducts, 4);
assertEquals(590d,
Arrays.stream(mostValueableProducts)
.mapToDouble(arr -> arr[2]).sum(),0);
The test is expecting a result of 590 which corresponds to the final price of 3,73US$ (0.98+0.98+0.48+1.29). Once the algorithm sort by value the input array, we have the following result:
1
2
3
4
5
6
7
[1.0, 0.98, 230.0]
[5.0, 0.98, 230.0]
[7.0, 0.48, 75.0]
[4.0, 1.29, 55.0]
[2.0, 0.51, 30.0]
[3.0, 0.49, 28.0]
[6.0, 4.86, 14.0]
But here we realize the exists another combination of products which give us the most valuable products: 230+230+75+30+28 = 593 which corresponds to the final price of 3,44US$.
A greedy algorithm would sort the products by their “more grams per every dollar invested” ratio, and then select the product with the highest ratio that fits in the budget, and then repeat until the budget is achieved. This would give an approximate solution in linear time, but not necessarily the optimal one.
Then we need to refactor our code to calculate all combinations (subsets) and return the most valuable products under a budget of 4 US$.
The subsets can be represented by all the binary options from 0 to 7 (the array size).
1
2
3
4
5
6
7
0000 = {}
0001 = { {1, 0.98, 230} }
0010 = { {2, 0.51, 30} }
0011 = { {1, 0.98, 230}, {2, 0.51, 30} }
.
.
.
We build a hashMap to store all combinations and the sum of its values. Finally, we return the first element of the hashMap ordered by value
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
int len = myProducts.length;
int numIterations = (int) Math.pow(2, myProducts.length);
Map<double[][], Double> combinations = new HashMap<>();
for (int idx=0; idx<numIterations; idx++){
double[][] combx = new double[len][];
double sumPrice = 0;
double sumValue = 0;
int i = 0;
for (int idx2=0; idx2<len; idx2++) {
if ((idx & (int) Math.pow(2, idx2)) == 0) {
combx[i++] = myProducts[idx2];
sumPrice = sumPrice + myProducts[idx2][1];
sumValue = sumValue + myProducts[idx2][2];
}
}
if (combx.length > 0 && sumPrice <= budget) {
combinations.put(combx, Double.valueOf(sumValue));
}
}
You can see the complete solution explained in detail and all test cases in Cracking the Coding Interview
Please support me as a writer. Your donation will help add more articles to this website. Thank you!


