Graphs: Depth-First Search
Depth-First Search (DFS), is an algorithm to search for information in Graphs.
A Graph is a non-linear data structure consisting of nodes (or vertices) and edges. Its shape depends on the physical or abstract problem we are trying to solve. For instance, if nodes represent cities, then the routes which connect cities may be represented by no-directed edges. But if nodes represent tasks to complete a project, then their edges must be directed to indicate which task must be completed before another.
Graph theory was first proposed by Leonhard Euler when solved the Seven Bridges of Königsber problem.
Graphs: Terminology
To describe terms related to Graphs, we use the following Graph, which models Hyperloop transport to be installed in Germany, for instance.
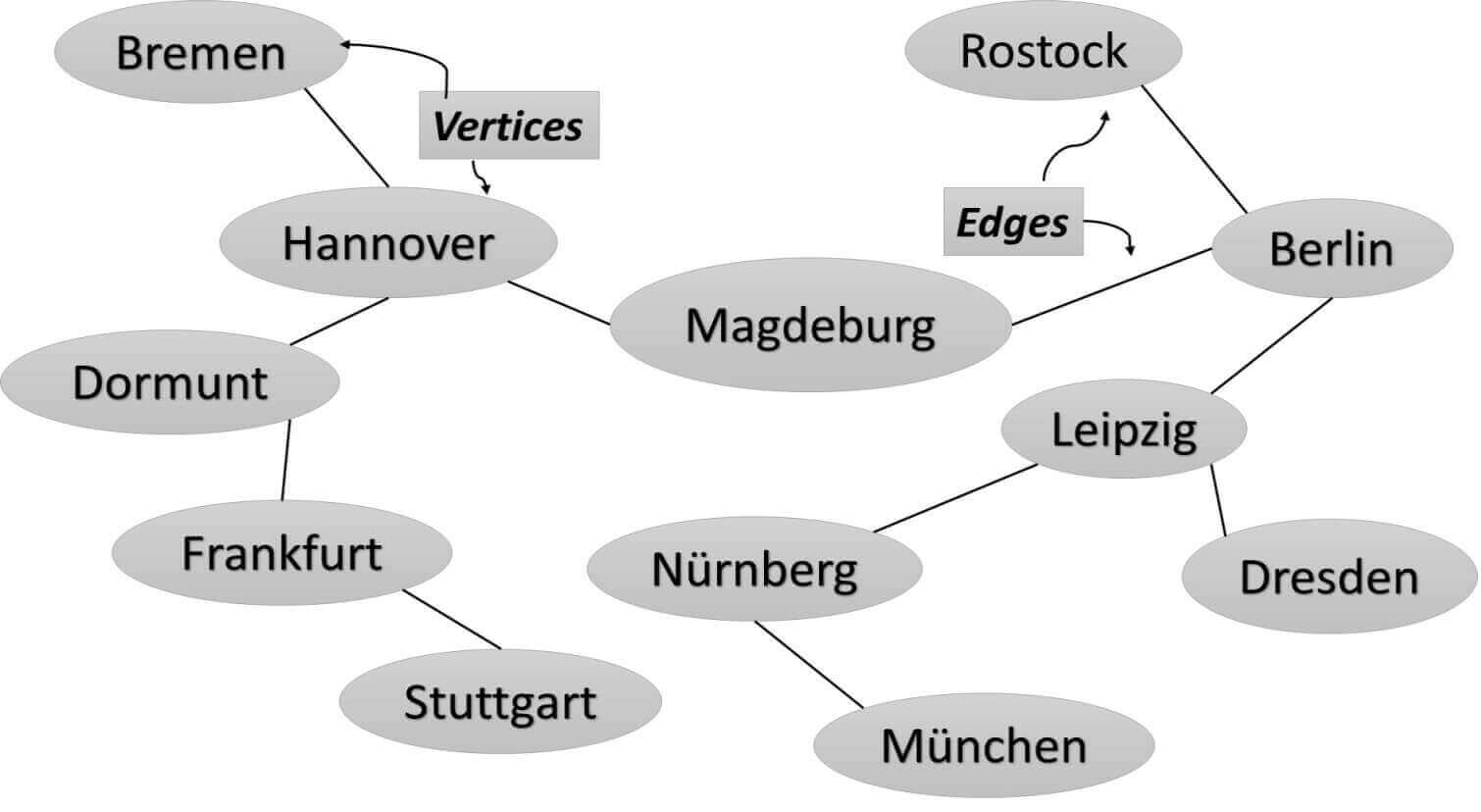
A Graph shows only the relationships between the vertices and the edges. Therefore, the most important here is to understand, which edges are connected to which vertex. Moreover, we can also say that Graph models connections between objects.
Adjacency
When two vertices are connected by a single edge, then they are adjacent or neighbors. In the figure above, the vertices represented by the cities Berlin and Leipzig are adjacent, but the cities Berlin and Dresden are not.
Path
A Path is defined as a sequence of edges. The figure above shows a path from Berlin to München, that passes through cities Leipzig and Nürnberg. Therefore, the path is Berlin, Leipzig, Nürnberg, München.
Connected Graphs
A graph is connected if exists at least one path from every vertex to every other vertex. Therefore, the figure above is connected because connects all cities.
Directed and Weighted Graphs
A graph is directed when the edges have a direction. In the figure above we have an undirected graph because the hyperloop can usually go either way. From Berlin to Leipzig is the same as from Leipzig to Berlin.
A tree is an undirected graph, as long as any two vertices are connected by exactly one path.
Graphs are called a weighted graph when edges are given weight. For instance, the distance between cities can be weighted in how fast they are connected. The edges may contain value/cost as well.
Acyclic Graphs Versus Cyclic Graphs
In Graphs, cycles are paths through edges and vertices that start and end at the same vertex. An acyclic graph has no such cycles.
Reasons to use Graphs
One of the questions that a graph can answer is: which cities can be reached from a specified city?. Well, to respond to this question, we need to implement search algorithms. There are two different ways of searching in a graph: depth-first search (DFS) and breadth-first search (BFS).
Depth-First Search (DFS)
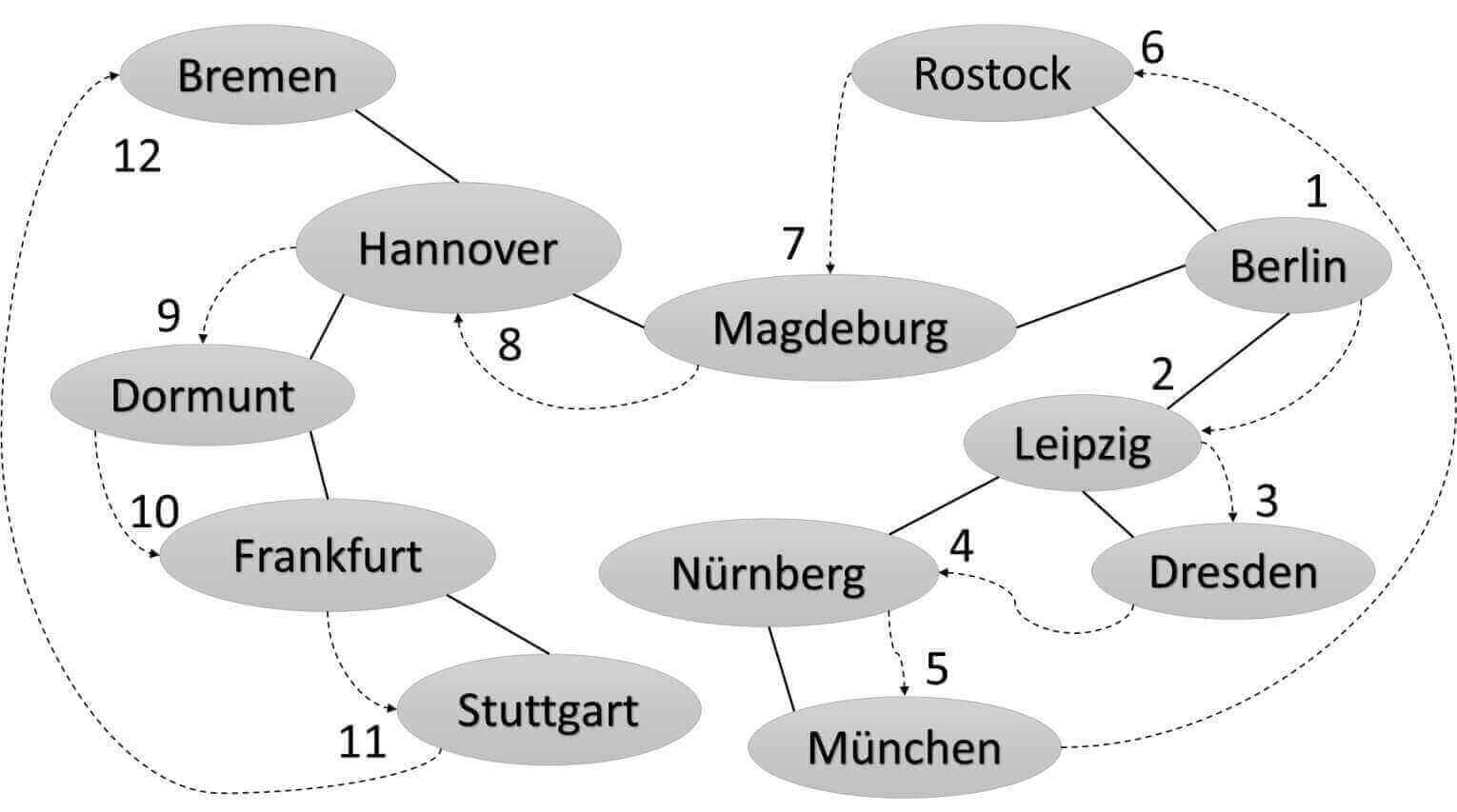
Depth-First Search (DFS) is an algorithm for traversing or searching for in a Graph. The algorithm starts at the root node (selecting some arbitrary city as the root node) and explores as far as possible along each path. The following Graph shows the sequence of cities followed by the DFS algorithm, if we choose Berlin as the root node, for instance.
Implementing Graphs Algorithm
We need an Object which supports any kind of data included in the Node (which includes the information, that we want to represent). We called it Vertex (because comes from a Mathematical concept). Moreover, to avoid searching in cycles, a boolean variable is included, so we will mark each node when we visit it.
1
2
3
4
5
6
7
8
9
public class Vertex {
private String name;
private boolean visited;
public Vertex(String name) {
this.name = name;
this.visited = false;
}
}
To define, that two vertices are connected (through edges), we have two approaches: the adjacency matrix and the adjacency list.
The Adjacency Matrix
In a graph of N vertices, we create a two-dimensional array of NxN. An edge between two vertices (cities) indicates a connection (two adjacent nodes) and is represented by 1. No connections are represented by 0.
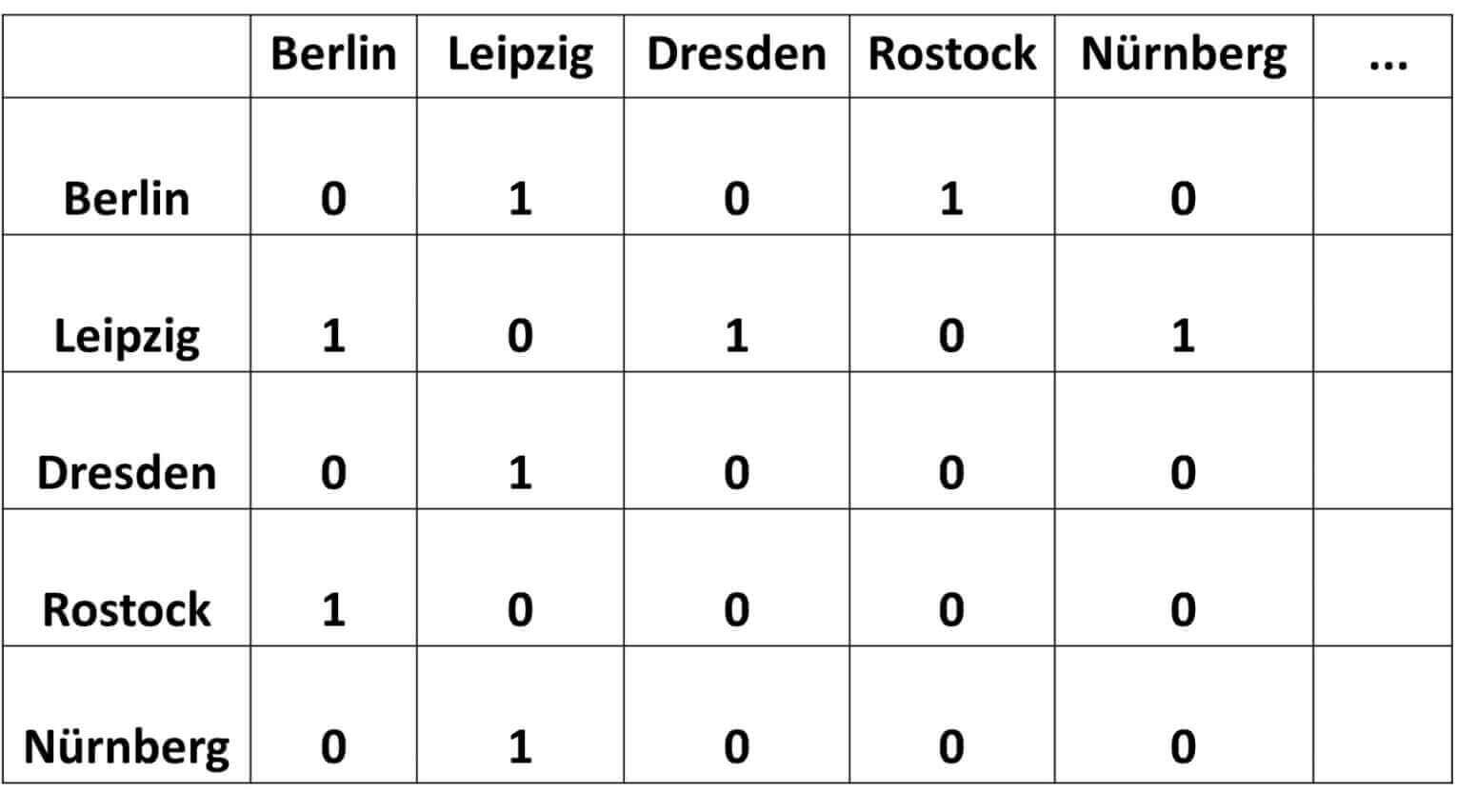
The table above says, Leipzig is adjacent to Berlin, Dresden, and Nürnberg, for instance.
Create and Initialize an Abstract Data Type
We create an Abstract Data Type called a Graph to define the behavior of our new data structure.
We need a stack data structure so we can remember the visited vertices. A stack follows the last-in, first-out (LIFO) principle, i.e., the city inserted at last is the first city to come out of the stack.
We define an arrayOfVertex[] array to store new Vertices(cities) added to the Graph.
We define a numOfVertices variable that indicates the number of Vertices already added to the Graph.
Since we will pass a String argument (city name) to our DFS algorithm, a mapOfVertex hashMap is defined to register the key-value: city-index, where the index is the City’s location at arrayOfVertex[].
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
public class Graph {
private final int MAX_VERTEX = 15;
private Vertex arrayOfVertex[]; //cities
private Map mapOfVertex;
//matrix of adjacent vertex:
private int matrixOfAdjVertex[][];
//register the location at the arrayOfVertex:
private int numOfVertices;
private Stack stack;
public Graph() {
arrayOfVertex = new Vertex[MAX_VERTEX];
mapOfVertex = new ConcurrentHashMap<>();
numOfVertex = 0;
matrixOfAdjVertex = new int[MAX_VERTEX][MAX_VERTEX];
stack = new Stack<>();
//initialize matrix
for (int i = 0; i < MAX_VERTEX; i++) {
for (int j = 0; j < MAX_VERTEX; j++) {
matrixOfAdjVertex[i][j] = 0;
}
}
}
}
Adding a Vertex
Before the implementation, we create a Test case with the following assumption:
1
2
3
4
5
6
@Test
public void test_addVertex() {
Vertex city = new Vertex("Berlin");
graph.addVertex(city);
assertTrue(graph.getMapOfVertex().size() ==1);
}
The implementation code register the new city in our mapOfVertex hashMap.
1
2
3
4
public void addVertex(Vertex city) {
mapOfVertex.put(city.getName(), numOfVertices);
arrayOfVertex[numOfVertices++] =city;
}
The numOfVertices variable determines the location (index) of the new City in the arrayOfVertex[].
Adding an edge
We add two entries to matrixOfAdjVertex, because two cities are connected in both directions.
1
2
3
4
5
6
public void addEdge(String city1, String city2) {
int start = mapOfVertex.get(city1);
int end = mapOfVertex.get(city2);
matrixOfAdjVertex[start][end] =1;
matrixOfAdjVertex[end][start] =1;
}
You can implement your code for these methods. The point here is that we need to define the topology of our Graph, adding Vertices(cities) and edges that connect them.
Depth-First Search: The algorithm
We define a dfs() method, which receives the City name as its argument. Then we locate the index of this city in our hashMap, is marked as visited, and push it onto the stack.
We iterate the stack until is empty. And this is what we do in every iteration:
- We retrieve the Vertex from the top of the stack (peek)
- We try to retrieve at least one unvisited neighbor for this vertex
- If one vertex is found, it is marked as visited and pushes it onto the stack
- If one vertex is not found, we pop the stack
If Berlin were our entry city, then the first adjacent city will be Leipzig, which is marked as visited and push it into the stack. In the next iteration, we read Leipzig (through peek method) from the stack and look for its neighbors. Therefore, following these iterations, we arrive at München. That is the in-depth essence of this algorithm: to explore as far as possible along each branch before continuing with a new one.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public void dfs(String city) {
int vertex = mapOfVertex.get(city);
arrayOfVertex[vertex].setVisited(true);
System.out.print(city + " ");
stack.push(vertex);
while (!stack.isEmpty()) {
int adjVertex = getAdjVertex(stack.peek());
if (adjVertex != -1) {
arrayOfVertex[adjVertex].setVisited(true);
System.out.print(
arrayOfVertex[adjVertex].getName() + " ");
stack.push(adjVertex);
} else {
stack.pop();
}
}
}
1
2
3
4
5
6
7
8
private int getAdjVertex(int vertex) {
for (int adj=0; adj<numOfVertices; adj++) {
if (matrixOfAdjVertex[vertex][adj] ==1 &&
arrayOfVertex[adj].isVisited() ==false)
return adj; //return first adjacent vertex
}
return -1; //not vertices found
}
Test case
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
@Test
public void test_dfs() {
String city1 ="Berlin"; String city2 ="Leipzig";
String city3 ="Dresden"; String city4 ="Nürnberg";
String city5 ="Hannover"; String city6 ="Rostock";
String city7 ="Dortmund"; String city8 ="Frankfurt";
String city9 ="Stuttgart"; String city10 ="München";
String city11 ="Magdeburg"; String city12 ="Bremen";
graph.addVertex(new Vertex(city1));
graph.addVertex(new Vertex(city2));
graph.addVertex(new Vertex(city3));
graph.addVertex(new Vertex(city4));
graph.addVertex(new Vertex(city5));
graph.addVertex(new Vertex(city6));
graph.addVertex(new Vertex(city7));
graph.addVertex(new Vertex(city8));
graph.addVertex(new Vertex(city9));
graph.addVertex(new Vertex(city10));
graph.addVertex(new Vertex(city11));
graph.addVertex(new Vertex(city12));
graph.addEdge(city1, city2);
graph.addEdge(city2, city3);
graph.addEdge(city3, city4);
graph.addEdge(city4, city10);
graph.addEdge(city11, city5);
graph.addEdge(city5, city7);
graph.addEdge(city7, city8);
graph.addEdge(city8, city9);
graph.addEdge(city1, city6);
graph.addEdge(city1, city11);
graph.addEdge(city5, city12);
graph.dfs(city1);
}
Here, the output:
1
Berlin Leipzig Dresden Nürnberg München Rostock Magdeburg Hannover Dortmund Frankfurt Stuttgart Bremen
We can change the entry city and see different traversing paths
1
Hannover Dortmund Frankfurt Stuttgart Magdeburg Berlin Leipzig Dresden Nürnberg München Rostock Bremen
You can see as well the Breadth-First Search (BFS) algorithm by using an Adjacency List based on a LinkedList data structure in the following link

