Moises Gamio
Moises Gamio Software Engineer. Comprehensive experience in all phases of the software development lifecycle for several economic sectors.

Given N, find the smallest number with the same digits

Given N, find the smallest number with the same digits

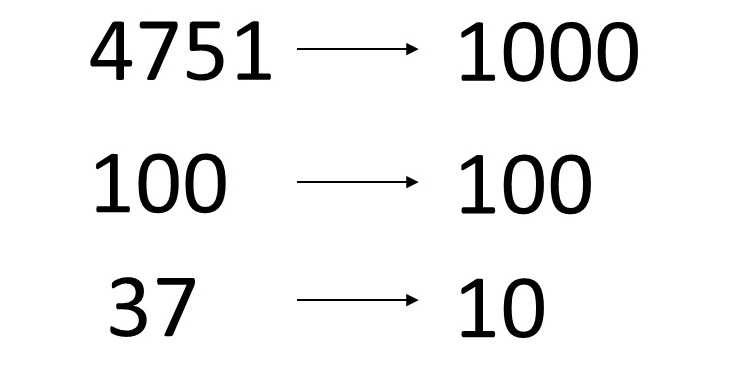
Write a method that, given an original number N, returns the smallest number with the same number of digits.

For instance, given N=4751, the method returns 1000. Given N=100, the method should return 100. Given N=1, the method should return 0.

Maybe the first idea comes to our minds could be to iterate from the given original number and decrease one by one, and in every iteration to check if every new number contains one digit less than the original number, if the answer is true, then the previous one is the smallest number.

Define a test case to validate what your code will do

Our assumption based on a test case:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

public class SmallestNumberTest {

  @Test
  public void test_right_smallest_values() {
    assertTrue(NumberUtils.smallest(4751) == 1000);
    assertTrue(NumberUtils.smallest(189) == 100);
    assertTrue(NumberUtils.smallest(37) == 10);
    assertTrue(NumberUtils.smallest(1) == 0);
  }

  @Test
  public void test_wrong_smallest_values() {
    assertFalse(NumberUtils.smallest(8) == 1);
    assertFalse(NumberUtils.smallest(2891) == 2000);
  }
}

Here, is the implementation code that works for positive numbers:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

public class NumberUtils {
  public static int smallest(int N) {
    int smallestNumber = 0;
    if (N <= 1)
      return smallestNumber;
    
    int numberOfDigitsOriginalN = String.valueOf(N).length();
    while (N > 0) {
      N--;
      if (String.valueOf(N).length() ==
          (numberOfDigitsOriginalN -1)) {
        return ++N;
      }
    }
    return smallestNumber;
  }
}

If we realize, the solution follows a common pattern:

N = 3891 -> smallest number = 1000

N = 189 -> smallest number = 100

N = 37 -> smallest number = 10

The smallest number is a power of 10, where the exponent is:

(number of digits of the given N – 1)

If we want to include negative numbers, we must consider the smallest number with the same number of digits and the same sign. We add our test case for negative numbers as well:

1
2
3
4
5

@Test
  public void test_right_smallest_values() {
  assertTrue(NumberUtils.smallest4(-1) == -9);
  assertTrue(NumberUtils.smallest4(-37) == -99);
}

Here, is the algorithm for positive and negative numbers:

1
2
3
4
5
6
7
8
9
10
11
12
13

public class NumberUtils {
  public static int smallest(int N) {
    int numberOfDigits = (int) String.valueOf(Math.abs(N)).length();
    if (N >= 0) {
      if (numberOfDigits == 1) {
        return 0;
      } else {
        return (int) Math.pow(10, numberOfDigits - 1);
      }
    } else
      return 1 - (int) Math.pow(10, numberOfDigits);
  }
}

The main idea in Analysis of Algorithms is always to improve the algorithm performance by reducing the number of steps and comparisons. The simpler and more intuitive an algorithm is, the more useful and efficient it will be.

Similar questions you can find in my book about algorithms and data structures. Learn how to apply common algorithms to the practical problems.

java interview