Merge two sorted lists algorithm

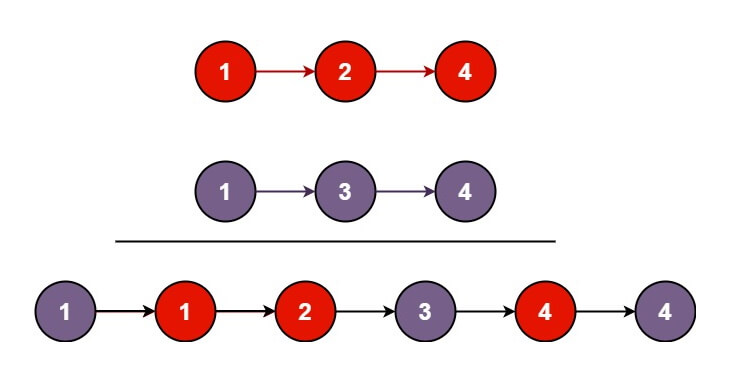
A merging algorithm takes two sorted lists as input and produces a single list as output, containing all the elements of the two inputs lists in sorted order.

A List is an abstract data type that can store a list of items. Unlike traditional arrays, however, lists can be expanded and shrunk and are stored dynamically in memory.

Problem

Given two sorted lists, merge them in a new sorted list.

Solution

We can join the two lists into a new list and apply a sort algorithm such as bubble sort, insertion, or quicksort. What we are going to do is to implement a new algorithm with a NlogN performance.

• We define a new List to add all elements from the other two lists in a sorted way.
• We define two indexes that point to every element in every list
• We iterate both lists while still exist elements in both lists
• We compare elements from both lists and add the smaller one to the new list in every iteration. Before passing to the next iteration, we increment in one the index of the list, which contains the smaller element.
• If there is a list that still contains elements, we add them directly to the new list.

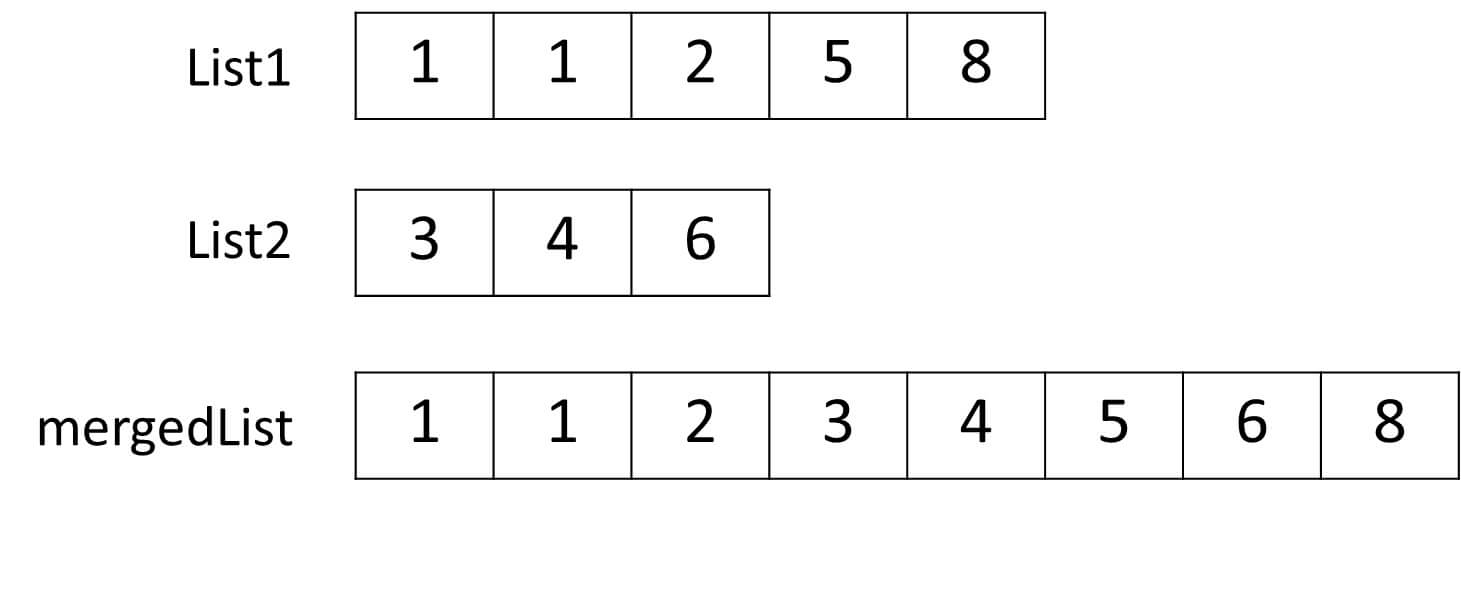
A test case helps to validate your assumptions

Our assumption based on a test case:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
@Test
public void mergeSortedLists() {
  List<Integer> sList1 = Arrays.asList(1,1,2,5,8);
  List<Integer> sList2 = Arrays.asList(3,4,6);
  assertEquals("[1, 1, 2, 3, 4, 5, 6, 8]",    
    SortedList.merge_sorted(sList1,sList2).toString());
}

@Test
public void mergeSortedLists2() {
  List<Integer> sList1 = Arrays.asList(2,4,5);
  List<Integer> sList2 = Arrays.asList(1,3,6);
  assertEquals("[1, 2, 3, 4, 5, 6]", 
    SortedList.merge_sorted(sList1,sList2).toString());
}

Merging sorted lists in a single pass

Here, the implementation code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public class SortedList {
  public static List<Integer> merge_sorted(
    List<Integer> sList1, List<Integer> sList2) {

    List<Integer> mergedSortedList = new ArrayList<>();
    int idx1 = 0;
    int idx2 = 0;

    while (idx1 < sList1.size() && idx2 < sList2.size()) {
      if (sList1.get(idx1) <= sList2.get(idx2)) {
        mergedSortedList.add(sList1.get(idx1));
        idx1++;
      } else {
        mergedSortedList.add(sList2.get(idx2));
        idx2++;
      }
    }

    return mergedSortedList;
  }
}

The previous algorithm is missing how to proceed when one of the lists still contains elements not compared. Keep reading here